· 気体の体積や分圧を含めた圧力や密度を求める計算問題の練習です。 アボガドロの法則により物質量(モル)や質量における比例関係を考えることになります。 状態方程式を使うことを基本にしておけば良いですが、標準状態での計算が多い容積を求める式は、 ×50×30= 答え これをL(リットル)になおすと、 1000 =1l だから =30L(リットル) となります。 答え 30L 教え方4 メートルなど大きな単位の体積について 教え方4-① 大きな直方体や立方体の体積を計算して求める方法に気づかせ、 (立方メートル)の単位を体積を計算で求める 式が立てられるね! 4 6× × 5 = 1 5 その② ( だん) 5 × 5 × 5 = 125 (答) cm³ その② 125 この学習を生かして、体積を計算で求めるには・・・ ① たて、横、高さをはかる ② 3つの辺の長さを表す数をかける。
容積 ようせき
体積を求める式
体積を求める式-積分式: V=8 ∫∫ (1-X2-Y2)1/2 dXdY (8分の1球の体積X8) 上記の積分式は、 体積を求める数値積分のベースにはなりますが、 解析的 に計 算するのは容易ではありません。 そのため、最初に説明したように 回転体 の体積 を求めるやり方で計算してみこの章では,理想気体の状態方程式を使ってシクロヘキサンC 6 H 12 の分子量を求める 8 液体のシクロヘキサンを回収し,フラスコの口まで水で満たし,その水を体積 v mL を測定する。 9 気圧計で,実験時の大気圧p hPaを測定する。 実験結果を確認しましょう。 シクロヘキサンの蒸気の質量は




体積の求め方ー四角柱ー 小学生 算数のノート Clear
(体積の計算) 立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し, x における断面積を S(x) とおきます. 上で復習した面積の求め方と同様にして一部が欠けた直円柱の体積 一部が欠けた直円柱の体積 一部が欠けた横倒し直円柱の半径と高さから体積、側面積、底面積、上面積を計算します。 中空円柱の体積 中空円柱の体積(液相)とすると、間隙部分の体積はVv=Va+Vw であり、土の前体積は V=Vv+Vsで表わされる。 与えられた土の間隙の状態を量的に表わすのに、土の全体積に対する間隙
立方体の体積は (1辺)×(1辺)×(1辺) で求めることができます。 だけど、これは直方体の (たて)×(よこ)×(高さ) これと全く同じものです。 全ての辺が同じ長さになってしまう立方体では、辺の区別をつけず たて、よこ、高さのそれぞれを · 立体の体積の求め方(公式)を一覧にまとめました。 公式を忘れてしまったときには、こちらで確認しましょう。 体積の求め方公式 立方体・直方体の体積の求め方 円柱の体積の求め方 三角柱の体積の求め方 円錐の体積の求め方 四角錐の体積の求め方 注意 スポンサードリンク (adsbygoogle小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 小学5年生の算数直方体と立方体を組み合わせた立体の体積を求める問題プリントを無料ダウンロード・印刷
(体積の計算) 立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し, x における断面積を S(x) · 半径rの球の体積を求める公式は、次のようになります。 πは円周率(=)です。 球の体積は、半径rの3乗に比例していくということですね! (例題) 半径5cmの球の体積は? 公式にr=5を · 表面積は半径の二乗に比例し,体積は半径の三乗に比例することは感覚的に明らかです。 よって,公式を覚えていなくても S = A r 2 , V = B r 3 S=Ar^2,\V=Br^3 S = A r 2 , V = B r 3 ということが分かります。




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成



1
· この公式は、これまでに説明してきた求め方にしたがうことで簡単に導くことができます。 (底面の円の面積)=(半径)×(半径)×(円周率)=r × r × π= πr 2 (円柱の体積)=(底面の円の面積)×(高さ)=πr 2 ×h= πr 2 h 円柱の体積を求めるには、与えられた半径や高さをこの公式に代入すればよいのです。 上の基本問題をこの公式を使って求める体積流量Qm 3 /sは、ある断面の面積Am 2 、平均流速vm/sとした場合、断面積と平均流速の積によって求めることができます。 体積流量Qm 3 /s=断面積m 2 ×平均流速m/s · っていう公式をつかえば、一発で体積を求めることができるんだ。 そんで、 底面積は、 半径×半径×円周率 だから、円周の体積はつぎの計算式で求められるよ。 半径×半径×円周率×高さ 円柱の体積の求め方がわかる2つのステップ




計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく



5年算数体積2わかる教え方
· 一次方程式長椅子の文章問題の解き方がわかる3ステップ 中2 >三角形acoがあってacを軸として回転させた体積を求める問題でその図形が円錐の底面積同士をくっつけた形なのですがどういう方程式を使えば答えが出せますか? 2つの円錐に分けて体積を計算するといいよ。 2つの正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積球の体積を求める公式は、V = 4/3 πr^3 で表されます。このページでは、例題と共に、この公式の使い方を説明しています。 このページでは、例題と共に、この公式の使い方を説明しています。




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun
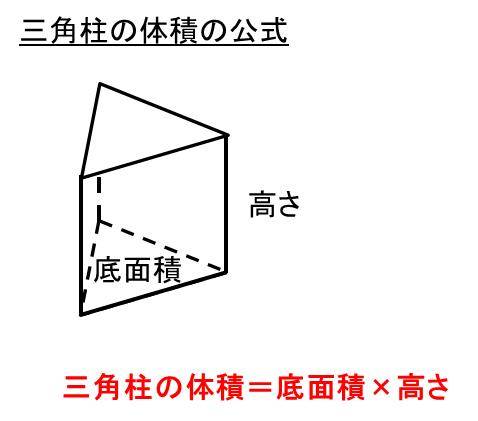



三角柱の表面積 底面積も と体積を求める公式と計算問題 単位との関係 ウルトラフリーダム
体積を求める式は? トレーニング 6×7×5 体積を求める式は? 体積を求めるときは、 たて×横×高さ、または 一辺×一辺×一辺の 3つをかけたらいいんだ。 「体積を計算で求められるようになった。もう1つずつ数えなくていいんだ!」 という感動をまとめよう! もしかして、㎤ の3って、 3回A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径の体積 V = πr2h V = π r 2 h 体積 = 半径 × 半径 × 314 × 高さ 公式の 導出 ( どうしゅつ ) 方法と計算例は、「 円柱の体積の求め方 」をご覧ください。 円柱の体積の求め方




円柱の表面積と体積を求める公式 具体例で学ぶ数学




体積の求め方ー四角柱ー 小学生 算数のノート Clear
このプリントでは, 体積に関する性質を用いて行列式の変形を説明する 別途講義で, 以下の 性質を改めて行列式の定義式から示す 立体の体積は a b c = 1 0 0 0 2 0 0 0 2 = 4 に等しい 注意もしa, b, c の中に同じベクトルがあると, 立体がつぶれて, 体積はゼロにまず体積v を求める式を立てる。 この定式化を「測定のモデル化」と言う。立て られた式は、測定のモデル式と呼ばれる。 まず、どの値の標準不確かさを求めるのか明確化する上でモデ ル式は、重要である。ここでは、mと 0の標準不確かさを求める。このときの式が であるが、この式は正規分布の式と似ている。 さて、この立体の体積を求める問題を考えると、一つは長方形による面積の応用で、直方体に分割することで体積を求めることができる。 しかし、横にスライスすることで、円盤(円筒)の体積を合計することでも体積が求め




小5 算数 小5 3 直方体と立方体の体積 Youtube




円錐の体積ってなんであの公式なの Webty Staff Blog
体積を求める式 体積=質量÷密度 質量:0g 密度:40g/cm 3 → 0÷40=5 → 体積は5cm 3 体積と密度から質量を求める 例えば密度の単位がg/cm 3 の場合、1cm 3 当たりの質量(g)なので、体積全体の質量を求めるためには、体積に密度を掛けることで求めることができます。式は 体積×密度=質量 で子育て 子育て では実際に、立方体や直方体の体積を求める問題を解いていきたいと思います。 問題① 次の立方体の体積を求めましょう。 《立方体の体積の求め方》 この立方体の1辺の長さは4cm。 立方体の体積=1辺×1辺×1辺であることから 求める立方体の体積『気体の体積は、圧力に反比例し、絶対温度に比例する』 というもので、 P:圧力 V:体積 R:気体定数 T:絶対温度で表した温度 とすると、 PV=RT ・・・・式2 で表されます。 式1と式2から気体中の音速を求める式が導かれます。




球の表面積と体積の公式 数学fun




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半体積を求める公式が使えるように、 に変形したり、 分けたりして考えている。 まとめ のような形の体積も、 下のような形の体積を、いろいろな方法で求めましょう。 ( ) ( ) 考え方① 考え方② 本山第二小学校5年 算数科 家庭学習課題ワークシートNo9円錐の体積の公式より, V = 1 3 π r 2 h = 1 3 π × 1 2 × 1 = π 3 定積分の公式を用いた場合 定積分の基本式より, ∫ a b f (x) d x = F (x) a b = F (b) − F (a) ( F (x) は f (x) の原始関数の1である ) 求める円錐の底面積 S (x) を S (x) = π {f (x)} 2 とすると,(これについて




三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ



算数科予習プリント 体積の求め方は考えられたかな 翁島 おきなしま 小学校ホームページ
· 積分計算による体積の求め方! 断面積の積分や回転体の体積 21年2月19日 この記事では、「立体の体積を積分計算で求める方法」についてわかりやすく解説していきます。 各種公式や問題の解き方なども説明していくので、ぜひこの記事を通して体積の公式は、柱体(ちゅうたい)は「底面積×高さ」、錐体(すいたい)は「底面積×高さ×1/3」で計算できます。 この2つを暗記すれば、体積の公式は簡単です。 但し、三角柱と円柱では「底面積の計算式」が違うので注意しましょう。 今回は、体積の公式の求め方、覚え方と一覧、三角柱、円柱、三角錐の体積について説明します。 体積の意味など下記も参考まず体積v を求める式 を 体積v のモデル式 モデル式を立てて、不確かさの要因を明ら かにする。それに相当する枠を作る。(それ ぞれの入力が複数の不確かさ要因をもつ ときには、段組みを工夫する必要がある。) 7 8 測定値の計算 1000 1003 999 997 1001 1000 g 5 1 1 1 n k m k n m 平均値を求める



U9j580gf8iba369ji2w Xyz P 296




体積の測定 測定のことを 即 知りたい ソクシリ キーエンス
· 体積を求めたい場合、「し・み・た」の「た」を隠して公式を思い出しましょう。 $$体積(㎤)=\frac{質量(g)}{密度(g/㎤)}$$ 公式を思い出したら、数を当てはめていくだけです。回転体の体積を求める公式 レベル ★ 入試対策;更新日時 y = f (x) y=f(x) y = f (x) , x = a x=a x = a , x = b x=b x = b , x x x 軸で囲まれた領域




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
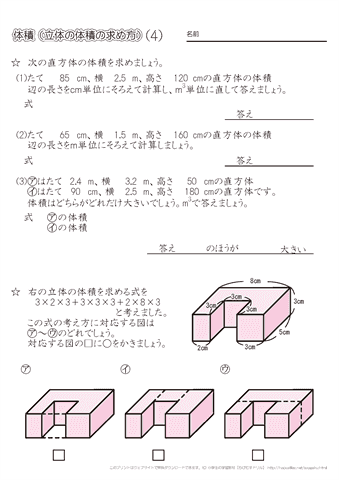



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ




3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ




立体の体積を求める公式




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




丸棒の重量 円柱の体積と重量の求め方 鉄の場合




2 5 Descubre Como Resolverlo En Qanda




小5 算数 小5 5 体積の求め方のくふう Youtube
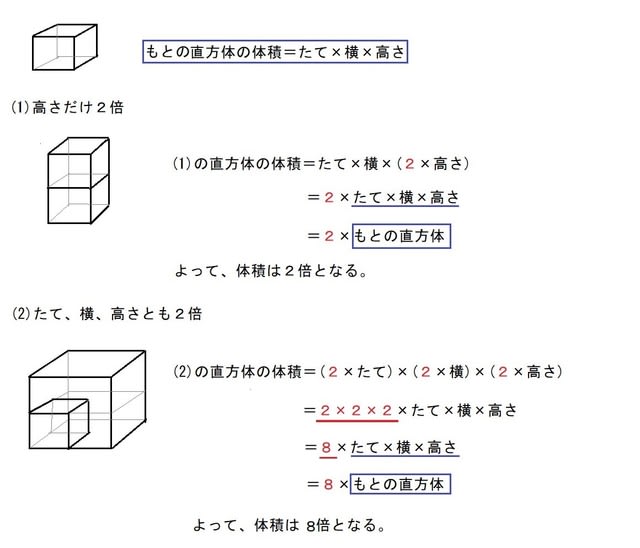



直方体 立方体の体積 小5 きちんと式を書けば簡単 算数の教え方教えますmother S Math Happy Study Support




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




円柱の体積の求め方 公式 小学生 中学生の勉強




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




体積の求め方 計算公式一覧
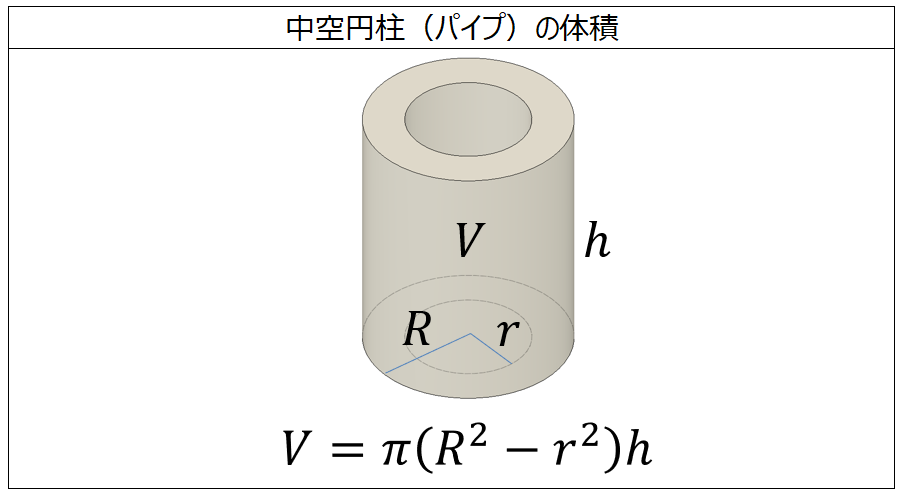



体積の計算 中空円柱 パイプ 製品設計知識




2 5 Descubre Como Resolverlo En Qanda



体積の公式は 1分でわかる求め方と覚え方 一覧 三角柱 円柱 三角錐の体積




円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ




体積 容積の求め方 算数 教科質問ひろば 進研ゼミ小学講座




6年算数立体の体積1 教え方




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン



立派な 台形 体積 求め 方



三角柱の体積を求める時にテキストでは2分の1と出ているんですがこれは何なんで Yahoo 知恵袋



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun
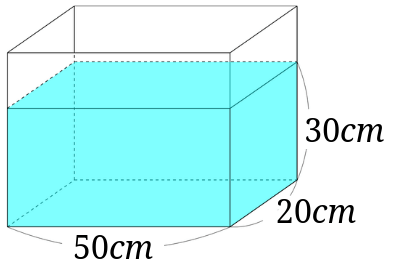



石を水の入った水槽に沈めて体積を求める問題の教え方 みけねこ小学校



地図の体積計測




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




体積の求め方 計算公式一覧




3分でなるほど 三角錐の体積 表面積の求め方をマスターしよう 数スタ




体積の求め方 公式一覧 小学生 中学生の勉強




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
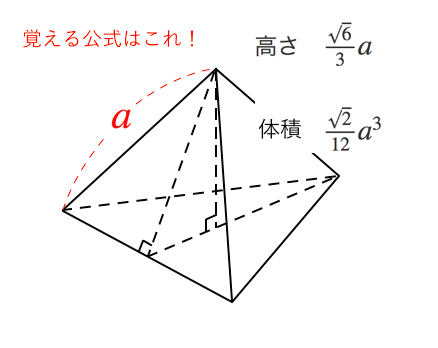



正四面体 高さ 面積を求める公式 苦手な数学を簡単に




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書
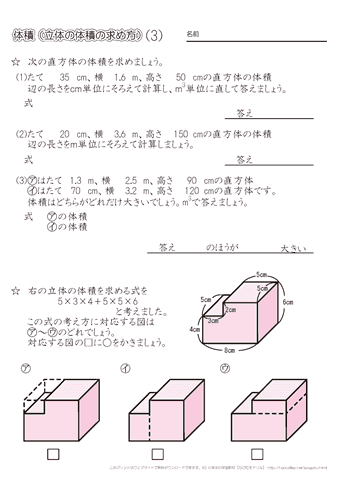



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




2 を途中式を含めて教えてください Clear




公式を図解 すい体の体積 円すいの表面積の求め方




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
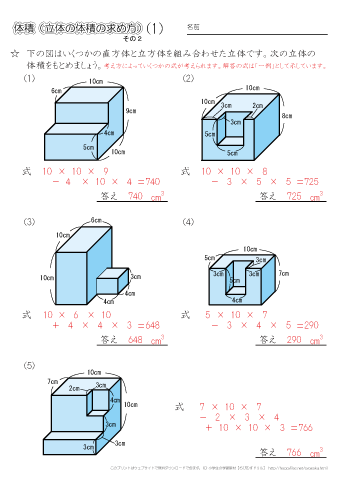



小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




水の質量と体積を変換 換算 する方法 計算問題を解いてみよう 水の重さの求め方




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




くふうして体積を計算しよう 家庭学習レシピ



1



5年算数体積2わかる教え方




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト
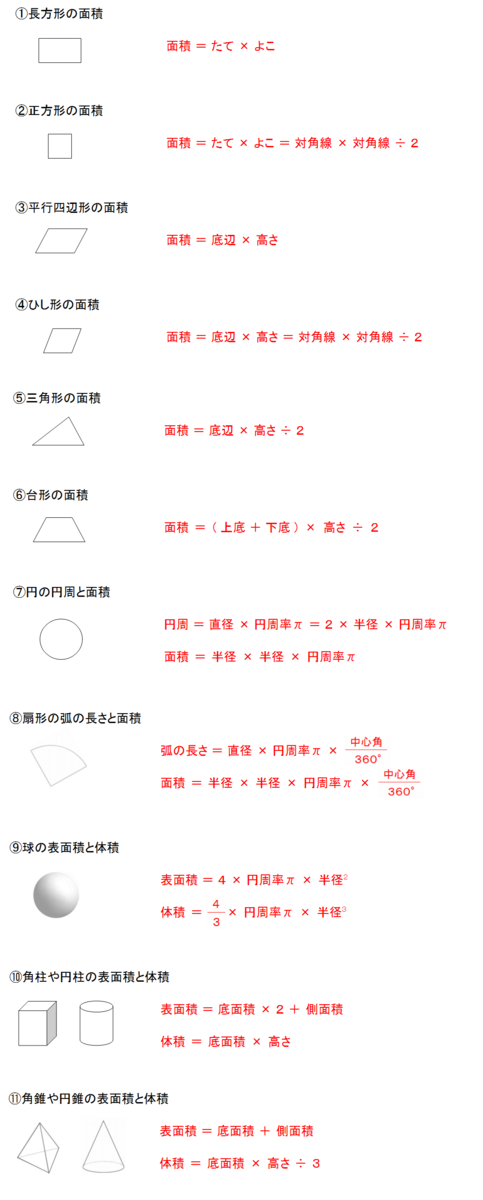



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師




球の体積と表面積 公式と計算問題と証明 Irohabook




石を水の入った水槽に沈めて体積を求める問題の教え方 みけねこ小学校




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun




体積 複雑な形の立体 算数 教科質問ひろば 進研ゼミ小学講座



算数流体積の求め方 Sciencelab 冨田塾




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



5年算数体積2わかる教え方




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun
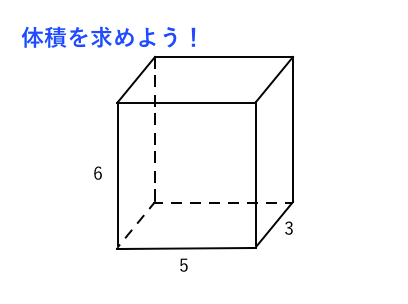



超簡単 体積の求め方 苦手な数学を簡単に




密度の公式 物質の密度の求め方は しみた の法則 中学理科 Yattoke 小 中学生の学習サイト




角柱の体積の公式 求め方は底面積と高さに注目するだけだ 中学や高校の数学の計算問題
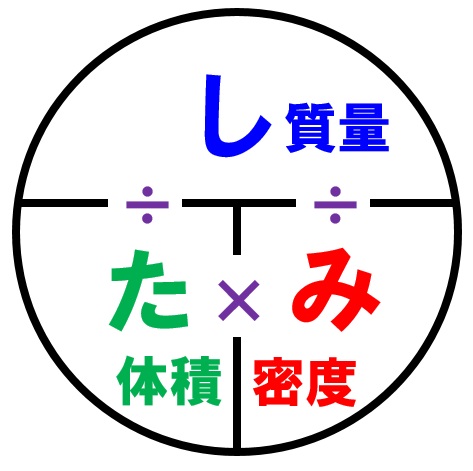



中1理科 密度の求め方3パターンの計算方法 Examee




私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館



円柱の求め方について なんですが 小学校でやったはずの円柱の体 Yahoo 知恵袋




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




体積の求め方 計算公式一覧




面積や体積のかけ算の順序 おかしな算数教育 身勝手な主張




三角柱の体積の求め方 小学生向けに問題使って解説するぞ 中学数学 理科の学習まとめサイト




円すい 円錐 の体積の求め方と問題 小学数学 Irohabook




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学



1




角柱の体積 Youtube



質量の求め方は 1分でわかる公式と求め方 体積 密度との関係 求め方




Descubre Como Resolverlo En Qanda
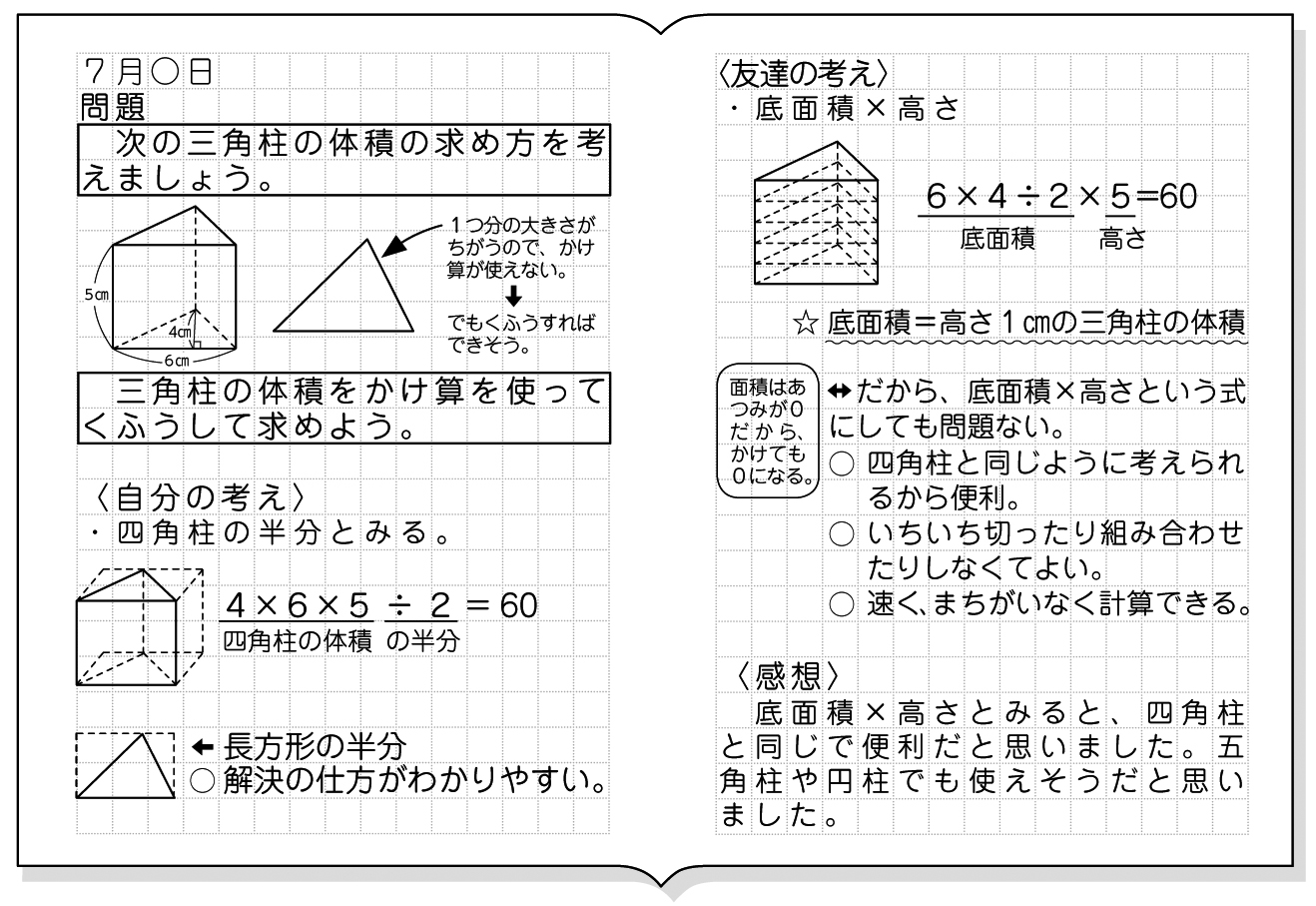



小6算数 角柱と円柱の体積 指導アイデア みんなの教育技術



容積 ようせき




公式を図解 すい体の体積 円すいの表面積の求め方



1




浮力の公式と計算方法まとめ 計算問題 体積の原理からの求め方 理系ラボ




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学
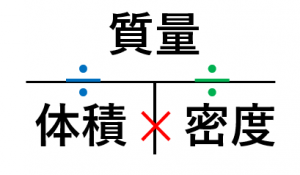



質量 密度 体積それぞれの求め方 具体例で学ぶ数学




体積の求め方 計算公式一覧
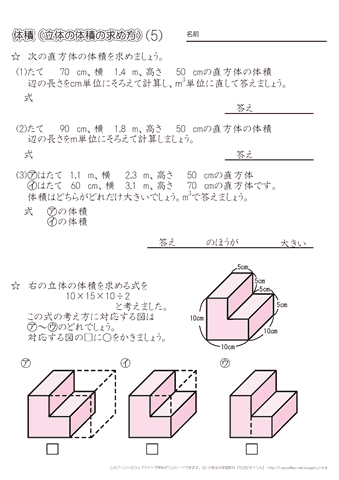



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生



質量と比重




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




小5 複雑な立体の体積 直方体 日本語版 Youtube




簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ


